MATHS, PROBABILITY

Quelques solutions aux problèmes du "PDF LLG"

15 min read

Page en léger, où le but est de résoudre les problèmes du famoso PDF LLG. J’essaie quand c’est possible de donner une solution différente de celle donnée dans le corrigé (semi) officiel et de faire le lien avec d’autres notions ou problèmes.

Liste des problèmes

  1. Exercice 174
  2. Exercice 266
  3. Exercice 287
  4. Exercice 318
  5. Exercice 389-390-392-393
  6. Exercice 391
  7. Interlude Facile d’accès

Exercice 174 (Une inégalité utile)

On cherche à montrer que pour tout $x \in \mathbb{R}^{+}$, $\sin(x) \leq x$ puis d’en déduire que pour tout $x \in \mathbb{R}$, $|\sin(x)| \leq |x|$.

💡 Solution a) La fonction sinus est bornée par $1$ et $-1$, pour $x$ positif, l'inégalité est donc évidente pour $x \geq 1$, le cas contentieux se situe pour $x \in [0, 1]$.
Dans ce cas-ci, on dérive (on peut le faire etc) deux fois la fonction $f : x \mapsto \sin(x)$, on obtient $f''(x) = -\sin(x) \leq 0$ pour $x \in [0, 1]$, la fonction sinus est donc concave sur cet intervalle et son graphe est en dessous de ses tangentes, en particulier en $x = 0$, dont l'équation de la tangente est $y(0) = f'(0) \times (x - 0) + f(0) = cos(0) \times x + 0 = x$
On aurait aussi pu étudier la fonction $f : x \mapsto \sin(x) - x$, dont la dérivée sur $\mathbb{R}^{+}$ est $f'(x) = \cos(x) - 1 \leq 0$ car $\cos(x) \leq 1$ pour tout $x \in \mathbb{R}^{+}$, donc $f$ est décroissante sur $\mathbb{R}^{+}$ et $f(x) = \sin(x) - x \leq f(0) = 0$ pour tout $x \in \mathbb{R}^{+}$ donc OK.

b) Si $x$ est positif alors on se ramène au cas précédent, si $x$ est négatif, on a $ \sin(-x) = - sin(x) \leq -x$. Cela se voit aussi graphiquement (par symétrie) :
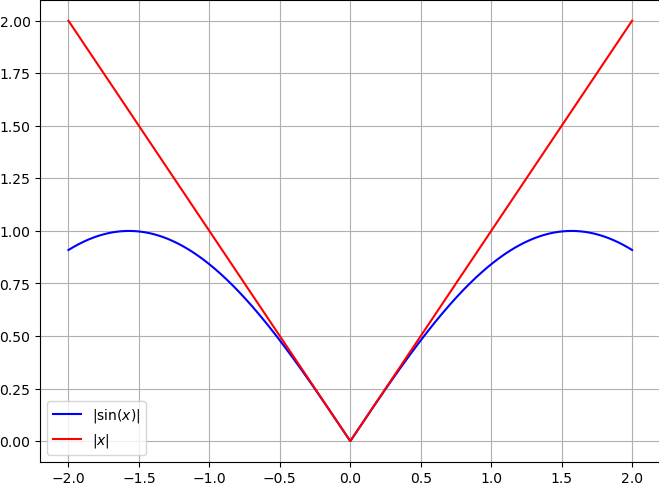
sinx_x


Ce que j'ai appris ?
Ce genre d'inégalité peut souvent se faire avec des arguments de convexité/concavité

Exercice 266 (Tout ce qui est possible finit par arriver)

On lance un dé non pipé. On répète $n$ fois l’opération, les lancers successifs étant supposés indépendants. Quelle est la probabilité $p_n$ pour que l’on obtienne au moins un 6 ? Déterminez la limite de $(p_n)_{n \geq 1}$.

💡 Solution On peut considérer l'événement contraire $\overline{A_{k}}$ : "ne pas obtenir 6 lors du k-ième lancer" dont la probabilité est $P(\overline{A_{k}}) = \dfrac{5}{6}$
N'obtenir aucun 6 lors des $n$ lancers est donc l'événement $\overline{A} = \cap_{k=1}^{n} \overline{A_{k}}$ dont la probabilité est, par indépendance des $\overline{A_{k}}$, $P(\overline{A}) = \prod_{k=1}^{n} P(\overline{A_{k}}) = \left(\dfrac{5}{6}\right)^n$
Finalement, la probabilité de l'événement qui nous intéresse $A$ : "obtenir au moins un 6 lors des $n$ lancers" est $p_n = 1 - P(\overline{A}) = 1 - \left(\dfrac{5}{6}\right)^n$, et la limite de $(p_n)_{n \geq 1}$ est donc $1$ (car $\left(\dfrac{5}{6}\right)^n \to 0$).
Tout ce qui est possible finit par arriver !!!

Ce que j'ai appris ?
Et voilà, c'était pas bien compliqué. On retiendra que passer au complémentaire est souvent un bon réflexe quand on voit le mot-clé "au moins".

Exercice 287 (Une application de Cauchy-Schwarz en probabilités)

Soit $n \in \mathbb{N}^*$, une expérience aléatoire peut produire $n$ résultats distincts notés $1, . . . , n$, de probabilités respectives $p1, . . . , pn$. On la répète deux fois de manière indépendante. On note $p$ la probabilité que les deux résultats soient égaux.

a) Exprimer $p$ en fonction des $p_{i}$ , $1 \leq i \leq n$.
b) En utilisant l’inégalité de Cauchy-Schwarz, montrer que $\frac{1}{n} \leq p$. Puis caractériser le cas d’égalité.

Highlight Text
On rappelle que l'inégalité de Cauchy-Schwarz s'écrit, pour des reéls $a_{1}, . . . , a_{n}$ et $b_{1}, . . . , b_{n}$ : $ | \sum_{i=1}^{n} a_{i}b_{i} | \leq \sqrt{\left(\sum_{i=1}^{n} a_{i}^{2}\right)}\sqrt{\left(\sum_{i=1}^{n} b_{i}^{2}\right)}$.
💡 Solution a) Pour que les deux résultats soient égaux, il faut que le premier résultat soit $i$ et le deuxième aussi, donc en sommant sur chaque possibilité, $p = \sum_{i=1}^{n} p_{i}^{2}$
b) Si l'on considère la somme $\sum_{i=1}^{n} \frac{p_{i}}{\sqrt{n}}$, on peut appliquer l'inégalité de Cauchy-Schwarz avec $a_{i} = p_{i}$ et $b_{i} = \frac{1}{\sqrt{n}}$.
Ce qui nous donne, en passant au carré, $\left(\sum_{i=1}^{n} p_{i} \frac{1}{\sqrt{n}}\right)^{2} \leq \left(\sum_{i=1}^{n} p_{i}^{2}\right)\left(\sum_{i=1}^{n} \frac{1}{\sqrt{n}}^{2}\right)$
Or, par a) $\sum_{i=1}^{n} p_{i}^{2} = p$ et $\sum_{i=1}^{n} (\frac{1}{\sqrt{n}})^{2} = \sum_{i=1}^{n} \frac{1}{n} = n \times \frac{1}{n} = 1$, donc $\left(\sum_{i=1}^{n} p_{i} \frac{1}{\sqrt{n}}\right)^{2} \leq p$.
Le membre de gauche peut se simplifier : $\frac{1}{n} (\sum_{i=1}^{n} p_{i})^{2} = \frac{1}{n}$ car $\sum_{i=1}^{n} p_{i} = 1$. On a donc bien $\frac{1}{n} \leq p$.

Il y a égalité si et seulement il existe $\lambda \in \mathbb{R}$ tel que $\forall i \in \{1, ..., n\}, p_{i} = \lambda \times \frac{1}{\sqrt{n}}$. On se doute bien que seul le cas possible est $p_{i} = \frac{1}{n}$. Un rapide calcul montre que c'est bien le cas.

Ce que j'ai appris ?
- Bien se rappeler de l'inégalité de Cauchy-Schwarz, elle est souvent utile en probabilités, un peu d'astuce pour faire apparaitre le $\frac{1}{n}$ et c'est bon.

Exercice 318 (Inégalité de Markov)

Soit $X$ une variable aléatoire positive. Montrer que pour tout $a > 0$, on a : $P(X \geq a) \leq \frac{\mathbb{E}(X)}{a}$

💡 Solution On a deux formules à notre disposition pour l'espérance :
$\mathbb{E}(X) = \sum_{x} x P(X = x)$ et $\mathbb{E}(X) = \sum_{\omega \in \Omega} X(\{\omega\}) P(\{\omega\})$
La première formule necessite de connaitre la loi de $X$ (et les valeurs $x$ possibles...), ce qui n'est pas le cas ici. Tout ce que l'on sait, c'est que $X$ est positive (idem pour $a$).
On a pas vraiment le choix, on va utiliser la deuxième formule, vu qu'on nous donne aussi un nombre $a$, on peut essayer de distinguer les éléments $\omega$ de $\Omega$ en deux parties : ceux pour lesquels $X(\{\omega\}) \geq a$ et ceux pour lesquels $X(\{\omega\}) < a$.

Ce qui nous permet d'écrire $$\mathbb{E}(X) = \sum_{\omega \in \Omega} X(\{\omega\}) P(\{\omega\}) = \sum_{X(\{\omega\}) \geq a}X(\{\omega\}) P(\{\omega\}) + \sum_{X(\{\omega\}) < a}X(\{\omega\}) P(\{\omega\})$$
La terme $\sum_{X(\{\omega\}) < a}X(\{\omega\}) P(\{\omega\})$ est positif ou nul (par définition de $X$) donc $$\mathbb{E}(X) \geq \sum_{X(\{\omega\}) \geq a}X(\{\omega\}) P(\{\omega\}) \geq a \sum_{X(\{\omega\}) \geq a} P(\{\omega\})$$

On remarque que $\sum_{X(\{\omega\}) \geq a} P(\{\omega\})$ est exactement la probabilité de l'événement $X \geq a$, par conséquent : $\mathbb{E}(X) \geq a P(X \geq a)$, ce qui nous donne bien l'inégalité de Markov.

Ce que j'ai appris ?
- L'inégalité en elle-même qui est utile dans plein de pbs
- Intuitivement, on sait que la moyenne est très sensible aux valeurs extrêmes, donc si on connait cette moyenne, on a une borne supérieure sur la probabilité d'avoir une valeur "extrême" (ici $a$). Par exemple, si on sait que la moyenne des notes d'une classe est $10$, on sait que la probabilité qu'un élève ait une note supérieure ou égale à $19$ est $\leq \frac{10}{19} \approx 0.52$...
- Jongler entre les deux formules d'espérance

Exercice 389 - 390 - 392 - 393 (Racines de l’unité)

Pour $n \in \mathbb{N}^{*}$, on note $U_{n}$ l’ensemble des racines $n$-ièmes de l’unité, c’est-à-dire les nombres complexes $z$ tels que $z^{n} = 1$, de la forme $z = e^{\frac{2i\pi k}{n}}$ avec $k \in {0, 1, . . . , n-1}$.
Si l’on représente ces racines dans le plan complexe, on obtient un polygone régulier à $n$ côtés inscrit dans le cercle unité, par exemple pour $n = 4, 5, 6$ :

r

a) Calculer la somme des elements de $U_{n}$
b) Calculer la somme des puissances p-ièmes des éléments de $U_{n}$
c) Pour $n \geq 2$ et $x \in \mathbb{R}$, calculer $S = \sum_{k=0}^{n-1} cos(x +\frac{2i\pi k}{n})$
d) Calculer le produit des éléments de $U_{n}$

💡 Solution a) Si $n = 1$, $U_{1} = \{1\}$ (une seule racine de l'unité...). Sinon, la somme des éléments de $U_{n}$ est $\sum_{k=0}^{n-1} e^{\frac{2i\pi k}{n}} = \sum_{k=0}^{n-1} (e^{\frac{2i\pi}{n}})^{k}$, on reconnaît la somme d'une suite géométrique de raison $q = e^{\frac{2i\pi}{n}}$ et de premier terme $1$, dont la somme est $\dfrac{1 - q^{n}}{1 - q} = 0$ car $q^{n} = e^{2 i \pi} = 1$. Cela se voit d'ailleurs graphiquement, les racines de l'unité sont les sommets d'un polygone régulier, donc par symétrie, la somme des racines est nulle (les vecteurs "s'annulant").

b) On suppose que $n > 1$ et p non nul, on a deux cas. Si $n$ divise $p$, c'est-à-dire si $p = n \times m$ pour un certain $m \in \mathbb{N}^{*}$, alors la somme est $$\sum_{k=0}^{n-1} e^{\frac{2i\pi k p}{n}} = \sum_{k=0}^{n-1} e^{\frac{2i\pi k m n}{n}} = \sum_{k=0}^{n-1} (e^{2i\pi})^{km} = n$$ Sinon, la somme est nulle par le même raisonnement qu'en a).
En fait si n divise p, on s'en convainc facilement, par exemple pour $p = 6$ et $n = 3$ (ici $U_{3} = {1, j, j^2}$), si on prends $j$, on a $j^{6} = (j^{3})^{2}$ et par definition de $j$, $j^{3} = 1$... Bref.
c) On pourrait uniquement utiliser des arguments de trigonométrie : $$\sum_{k=0}^{n-1} cos(x +\frac{2\pi k}{n}) = \sum_{k=0}^{n-1} cos(x)cos(\frac{2\pi k}{n}) - sin(x)sin(\frac{2\pi k}{n}) = cos(x) \sum_{k=0}^{n-1} cos(\frac{2\pi k}{n}) - sin(x) \sum_{k=0}^{n-1} sin(\frac{2\pi k}{n}) = cos(x) \times 0 - sin(x) \times 0 = 0$$ (En reconnaissant une somme télescopique, calcul complet ici).
Mais on peut aussi remarquer que notre somme vaut : $$S = \sum_{k=0}^{n-1} \Re(e^{i(x +\frac{2\pi k}{n})}) = \Re(\sum_{k=0}^{n-1} e^{i(x +\frac{2\pi k}{n})}) = \Re(e^{ix} \sum_{k=0}^{n-1} e^{i\frac{2\pi k}{n}}) = \Re(e^{ix} \times 0) = 0$$ (car la somme des racines de l'unité est nulle cf q d'avant + linéarité de la partie réelle).
d) Le produit est donné par $\prod_{k=0}^{n-1} e^{\frac{2i\pi k}{n}} = e^{\sum_{k=0}^{n-1} \frac{2i\pi k}{n}} = (e^{i \pi})^{n - 1} = (-1)^{n-1}$
On verifie bien que pour $n = 2$, $U_{2} = \{-1, 1\}$, le produit est $-1$ et pour $n = 3$, $U_{3} = \{1, j, j^{2}\}$, le produit est $1$.

Ce que j'ai appris ?
Ne pas oublier les cas particuliers, ici $n = 1$ et $p | n$... + Passer aux complexes pour simplifier les calculs puis prendre la partie réelle etc bon réflexe.

Exercice 391 (Inversion de Fourier discrète)

r
Flemme de LaTeX deso
💡 Solution Pas 36 solutions pour ce genre d'exercice, on plug la première formule dans la seconde et on regarde ce que ça donne. On a des choses qui ressemblent à des sommes de (puissances de) racines de l'unité, on se doute bien que l'on va devoir utiliser l'exercice précédent pour simplifier le bousin.
Le cas $n = 1$ se vérifie facilement, on considère ainsi $n > 1$ et $l$, $p$ $\in \{0, ..., n-1\}$ : $$ \begin{align} Z_{l} e{^\frac{2 i \pi l p}{n}} = \sum_{j=0}^{n-1}z_{j}e{^\frac{-2 i \pi j l}{n}}e{^\frac{2 i \pi l p}{n}} & = \sum_{j=0}^{n-1}z_{j}e{^\frac{2 i \pi l (p-j)}{n}} \end{align} $$ On injecte $(1)$ dans la seconde formule, ce qui donne : $$\frac{1}{n} \sum_{l=0}^{n-1}Z_{l} e{^\frac{2 i \pi l p}{n}} = \frac{1}{n} \sum_{l=0}^{n-1} \sum_{j=0}^{n-1}z_{j}e{^\frac{2 i \pi l (p-j)}{n}}$$ On échange les sommes (on peut le faire car les sommes sont finies) et on réarrange un peu les termes : $$\frac{1}{n} \sum_{l=0}^{n-1}Z_{l} e{^\frac{2 i \pi l p}{n}} = \frac{1}{n} \sum_{j=0}^{n-1}z_{j} \sum_{l=0}^{n-1} (e{^\frac{2 i \pi l}{n}})^{(p-j)}$$ Maintenant, si on prends un peu de recul, on voit que l'on additionne les $z_{j}$ pondérés par des coefficients qui ne sont rien d'autre que des sommes de racines de l'unité à la puissance $p-j$.
On peut utiliser l'exercice precedent pour calculer ces sommes, on a quelques cas à traiter :
  • $n = 1$, que l'on a déjà traité.
  • $n | p-j$, c'est-à-dire si $p-j = n \times m$ pour un certain $m \in \mathbb{N}^{*}$, alors la somme vaudrait $n$, ce qui est impossible car $p \leq n-1$ et $j \leq n-1$ donc $p-j \leq n-1$.
  • $j = p$, la somme vaut $n$ car $\sum e^{0}$...
  • Sinon, la somme vaut $0$ par le même raisonnement que l'exercice précédent.

En résumé, tous les coefficients devant les $z_{j}$ sont nuls sauf celui pour lequel $j = p$, et on a bien : $$\frac{1}{n} \sum_{l=0}^{n-1}Z_{l} e{^\frac{2 i \pi l p}{n}} = \frac{1}{n}(0 + n \times z_{p}) = z_{p}$$ ce qui montre la formule d'inversion de Fourier (discrète).

Ce que j'ai appris ?
  • Ne pas avoir peur de se lancer dans des calculs qui ont l'air compliqués à première vue, souvent on peut simplifier les choses en utilisant les bonnes propriétés.
  • Faudrait que je relise un peu sur la DFT et la FFT, ptet ce site qui a l'air bien

Interlude Facile d’accès (Nombres Complexes)

Le boss du youtube-game nous propose quelques exos sur les nbrs complexes

  • 1) Calculer en fonction de $n$ : $i^{n}$, $i + i^{2} + ... + i^{n}$ et $i \times i^{2} ... \times i^{n}$
  • 2) Trouver les nbrs complexes $z$ tq $(z - 2)(\overline{z} + i) \in \mathbb{R}$
  • 3) Pour $z$ complexe, quelle condition pour que tous $x$, $y$ réels : $$x + zy = 0 \Leftrightarrow x = y = 0$$
💡 Solution 1) On sait que $i^{n}$ a un cycle de longueur 4 : $i, -1, -i, 1, i....$ donc $i^{n} = i^{r}$ avec $r$ le reste de la division eucl de $n$ par $4$. Formule compacte pour $n = 2k$ pair, $i^{n} = (-1)^{k}$ sinon pour $n = 2k + 1$ impair, $i^{n} = i \times (-1)^{k}$.
On a simplement $$\prod_{k=1}^{n} i^{k} = i^{\sum_{k=1}^{n}k} = i^{\frac{n(n + 1)}{2}}$$ On se ramène au cas $i^n$ en regardant le reste de la div eucl de $\frac{n(n + 1)}{2}$ par $4$
Pour la somme $\sum_{k=1}^{n} i^{k}$, on reconnait une suite geo de raison $i$ donc $$\sum_{k=1}^{n} i^{k} = i \times \frac{1 - i^{n}}{1 - i}$$ C'est un bon reflexe de multiplier par le conjugué pour virer $i$ au dénominateur ce qui nous donne $$\sum_{k=1}^{n} i^{k} = \frac{i - 1}{2} \times (1 - i^{n})$$ On calcule la somme suivant le cycle de $i^{n}$ cf ci-dessus
2) On calcule $(z - 2)(\overline{z} + i) = z\overline{z} + iz - 2\overline{z} - 2i = |z|^{2} + i(z - 2) - 2\overline{z} = |z|^{2} - 2a - b + i(a - 2 +2b)$ ($z = a + ib$...). Ce nombre est réel ssi sa partie imaginaire est nulle, c'est-à-dire $a - 2 + 2b = 0 \Leftrightarrow b = 1 - \frac{a}{2}$. La droite d'eq $y = 1 - \frac{x}{2}$ est solution.
3) Soit $z \in \mathbb{C}$, il s'écrit ainsi $z = a + ib$ avec $a,b$ réels. On a donc $$x + zy = x + (a + ib)y = (x + ay) + i(by)$$ Si $z \in \mathbb{R}$ c'est-à-dire $b = 0$ alors $$x + zy = 0 \Leftrightarrow x + ay = 0$$ On a par ex $a = \frac{-x}{y}$ solution avec $y$ non nul. Réciproquement si $z$ n'est pas réel, alors $$x + zy = 0 \Leftrightarrow (x + ay) + i(by) = 0$$ En identifiant partie réelle et imaginaire on a bien $x = y = 0$. Rédaction un peu degueue mais on voit bien que graphiquement si on a un nombre complexe qui n'est pas sur la droite des réels, la seule transformation affine qui le ramènerait sur cette droite est $z \times 0 + 0$..

Ce que j'ai appris ?
- Garder en tête le cycle des puissances de $i$ + tjrs identifier partie réelle et imaginaire pour les exos sur les nbrs complexes + $z\overline{z} = |z|^{2}$ + mult par le conjugué pour simplifier les fracs