Topological Sorting And Autograd
Firms love to force candidates to go through bizarre humiliation rituals during interviews. One of these was to implement a topsort algo for their autograd engine.
If we consider a computation graph where each node represents a variable and each edge represents a dependency, the goal of this algorithm is to sort the nodes in “topological order”, i.e. such that if there is an edge from node \(u\) to node \(v\), then \(u\) comes before \(v\) in the sorted list of nodes. (The topsort alg only works on directed acyclic graph (DAG), directed because the whole point is to sort dependencies, and acyclic because otherwise we’d run into contradictions.)
As an example, if we have the following graph :
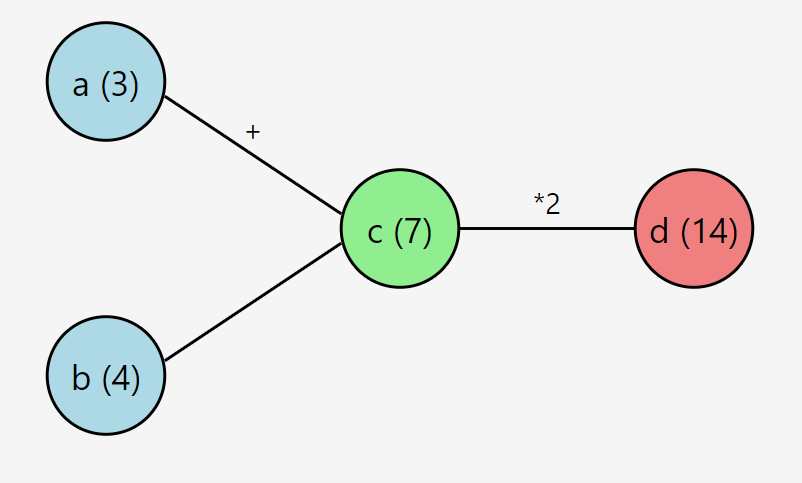
Then the expected output would be ['a', 'b', 'c', 'd'] or ['b', 'a', 'c', 'd'] since c depends on both a and b and d depends on c.
DFS
Main tool to solve this problem is the Depth First Search (DFS) algorithm.
Quick explanation, courtesy of Claude:
- You start in one room.
- You look around and see all the doors in the room.
- You pick one door and go through it into the next room.
- In this new room, you do the same thing: look for doors and pick one.
- You keep doing this, always choosing a new door if there is one.
- Sometimes you'll end up in a room with no new doors (all doors lead to rooms you've already visited). When this happens, that means you've reached the "furthest" room, you go back to the previous room.
- In the previous room, you look for any doors you haven't gone through yet. If you find one, you go through it.
- If there are no new doors in that room either, you go back again.
- You keep doing this until you've visited every single room and tried every single door.
The key ideas are:
- Always go as deep as you can before coming back.
- Keep track of which rooms you've visited so you don't go in circles.
- When you can't go forward anymore, you go back (this is called "backtracking").
A simple implementation of the DFS algorithm in Python would look like this :
# A graph is defined as a dictionary where the keys are the nodes and the values are the children of the node
graph = {
'a': ['c'],
'b': ['c'],
'c': ['d'],
'd': []
}
# Not relevant because we use a recursive implementation but DFS = stack (LIFO) and BFS = queue (FIFO) in their iterative implementations
stack = []
# Dictionary to keep track of the visited nodes
visited = {node: False for node in graph}
def dfs(graph, node, visited, stack):
visited[node] = True
for children in graph[node]:
if not visited[children]:
dfs(graph, children, visited, stack)
stack.append(node)
for node in graph:
if not visited[node]:
dfs(graph, node, visited, stack)
print(stack)
# >> ['d', 'c', 'a', 'b']
In the main loop, we iterate over all nodes in the graph and call dfs. The dfs appends the current node to the stack only after all its children have been visited. So that would be :
a-> dfs(c) -> dfs(d) (forward) -> append(d) -> append(c) (backtrack) -> append(a) (finally append current node)b-> dfs(c) (already visited so we stop here) -> append(b) (append current node)
All nodes have been visited and our stack is ['d', 'c', 'a', 'b']
For the sake of completeness, here is the iterative version of the DFS algorithm :
def dfs_iterative(graph):
visited = {node: False for node in graph}
result = []
# In case of a disconnected graph
for start in graph:
if not visited[start]:
stack = [start]
while stack:
node = stack.pop()
if not visited[node]:
visited[node] = True
result.append(node)
stack.extend([child for child in graph[node] if not visited[child]])
return result
Top Sort
Top sort is just a small modification of the DFS algorithm. Instead of appending the current node to the stack as soon as we visit it, we append it only after we’ve visited all its children. This ensures that the nodes are sorted in the correct order.
Since we want to use this stuff in the context of an autograd engine, we’ll represent the graph a bit differently. Instead of a dictionary, we’ll just define Nodes, each Node has a list of parents and a value / computation.
class Node:
def __init__(self, name, value, parents=None):
self.value = value # The value of the node (e.g., the result of a computation)
self.parents = parents if parents else [] # Nodes this node depends on (inputs)
self.grad = 0 # Gradient for backpropagation
self.name = name # node ID
def __repr__(self):
return f"Node({self.name} : {self.value})"
def topsort(nodes):
visited = set()
sorted_nodes = []
def dfs(node):
if node in visited:
return
visited.add(node)
for parent in node.parents:
dfs(parent)
sorted_nodes.append(node)
for node in nodes:
dfs(node)
return sorted_nodes[::-1] # Reverse the list to get the correct order
# Our graph as a list of nodes
a = Node("a", 3)
b = Node("b", 4)
c = Node("c", a.value + b.value, parents=[a, b]) # c = a + b
d = Node("d", c.value * 2, parents=[c]) # d = c * 2
nodes = [a, b, c, d]
print(topsort(nodes))
# >>> [Node(d : 14), Node(c : 7), Node(b : 4), Node(a : 3)]
Why is it useful ? If we have a topologically sorted computation graph, we can easily compute the gradients of each node with respect to the final output by going through its dependencies in reverse order. This is the basis of the backpropagation algorithm used in neural networks. Something like that :
import math
class Node:
def __init__(self, value, parents=None, operation=None):
self.value = value
self.parents = parents if parents else []
self.operation = operation
self.grad = 0.0
self.backward = lambda: None
def __repr__(self):
return f"Node(value={self.value}, grad={self.grad})"
def topsort(node):
visited, sorted_nodes = set(), []
def dfs(n):
if n not in visited:
visited.add(n)
for parent in n.parents:
dfs(parent)
sorted_nodes.append(n)
dfs(node)
return sorted_nodes
# Go through the sorted nodes in reverse order and compute gradients
def backward(node):
sorted_nodes = topsort(node)
node.grad = 1.0
for n in reversed(sorted_nodes):
n.backward()
# Basic operations and their gradients
def add(a, b):
out = Node(a.value + b.value, parents=[a, b], operation='+')
def _backward():
a.grad += out.grad
b.grad += out.grad
out.backward = _backward
return out
def substract(a, b):
out = Node(a.value - b.value, parents=[a, b], operation='-')
def _backward():
a.grad += out.grad
b.grad -= out.grad
out.backward = _backward
return out
def multiply(a, b):
out = Node(a.value * b.value, parents=[a, b], operation='*')
def _backward():
a.grad += b.value * out.grad
b.grad += a.value * out.grad
out.backward = _backward
return out
def power(a, x):
out = Node(a.value ** x, parents=[a], operation=f'**{x}')
def _backward():
a.grad += x * (a.value ** (x - 1)) * out.grad
out.backward = _backward
return out
def sqrt(a):
out = Node(math.sqrt(a.value), parents=[a], operation='sqrt')
def _backward():
a.grad += out.grad / (2 * math.sqrt(a.value))
out.backward = _backward
return out
def exp(a):
out = Node(math.exp(a.value), parents=[a], operation='exp')
def _backward():
a.grad += out.value * out.grad
out.backward = _backward
return out
def log(a):
out = Node(math.log(a.value), parents=[a], operation='log')
def _backward():
a.grad += out.grad / a.value
out.backward = _backward
return out
# etc....
a = Node(2)
b = Node(6)
Q = substract(power(a, 3), power(b, 2)) # Q = a^3 - b^2
# Forward pass
print(f"Forward pass result: {Q.value}")
# Backward pass
backward(Q)
print("Gradients:")
for node, name in zip([Q, b, a], "Qba"):
print(f"{name}: {node.grad}")
# >>> Forward pass result: -28
# >>> Gradients:
# >>> Q: 1.0
# >>> b: -12.0
# >>> a: 12.0
We can quickly double-check our results with PyTorch :
import torch
a = torch.tensor([2.], requires_grad=True)
b = torch.tensor([6.], requires_grad=True)
Q = a**3 - b**2
Q.backward()
print(Q)
# >>> tensor([-28.], grad_fn=<SubBackward0>)
print(a.grad, 3*a**2 == a.grad)
print(b.grad, -2*b == b.grad)
# >>> tensor([12.]) tensor([True])
# >>> tensor([-12.]) tensor([True])
tl;dr :
